6. A BIOKÉMIAI FOLYAMATOK
A biológiai szűrés hatásmechanizmusa a szennyező molekulák lebontásán alapszik. A szűrés azáltal jön létre, hogy szennyező molekula átalakul, miáltal nem számít már szennyezésnek.
A 2.3-4. táblázat a biokémiai folyamat fenntartásaként a baktériumok életösztönét jelöli meg. A sommás kijelentésnek azonban mélyebb oka van.
6.1 Sejtek tápanyagcseréje
A biofilmen belüli tápanyag-lebontás – ha annak csupán a megtörténtét regisztráljuk – egyszerű dolognak látszik. Belenagyítva a képbe, lényegesen árnyaltabb lefolyást kapunk. A biológusok által már jó ideje tisztázott működési mechanizmust érdemes a rendszertechnikai összefüggések megértése érdekében röviden felidézni.
Mint minden élőlénynek életműködésük fenntartásához - így az egysejtű baktériumoknak is -energiára van szükségük. Molekulák elbomlásakor energia szabadul fel, más szavakkal a tápanyag-lebontási folyamat exoterm. A „törekvés a felszabaduló energia megszerzésére” életösztönként nyilvánul meg.
A molekulák – így a víz szennyezettségét okozó molekulák is - a természetben általában stabil képződmények. Stabilitásukat az aktiválási energiaszint teremti meg. Ahhoz, hogy elbonthatók legyenek ΔEaktiválási energia közlése szükséges. Enzimek jelenlétében azonban ez a küszöbérték lecsökken és a molekula könnyebben átalakul, lehetővé téve újabb, kisebb molekulák, ún. bomlástermékek létrejöttét.


6.1‑1. ábra Az enzimkatalizáció hatása és annak szemléltetése
A reakció idő elteltével a víz szennyezését okozó szubsztrát termékké válik, miközben energia szabadul fel. A felszabaduló energiához való hozzáférés lehetősége jelenti a tápanyag-lebontási folyamat tulajdonképpeni hajtóerejét.
A 6.1-1. ábra jobb felén analógiaként egy poharat látunk. A mély pohár alján a folyadék stabil állapotban van, lapos pohárból azonban könnyen kiloccsan. Az enzimkatalizáció tkp. a pohár falának magasságát csökkenti, analóg módon az aktiválási energiaszintet mérsékli, lehetővé téve a molekula könnyű elbomlását. Az enzimek a reakció szabadenergia változását (ΔE) azonban nem befolyásolják. A természet az enzimeknek ezt a képességét használja a víz megtisztításához is.
Feynman Mai Fizika I. / A modern természettudomány alapjai című könyvében minderről a következőképpen érvel:
„A kémiai reakciók legtöbbje tehát azért nem megy végbe, mert útját állja ennek
a dombtetőnek megfelelő aktivációs energia.
….
Az enzim jelenlétében végbemegy a reakció.
….az enzim közvetlenül nem vesz részt a reakcióban, nem változik meg, csupán
lehetővé teszi, hogy egy atom egyik helyről eljusson a másikba.”
A sejtek tápanyagcseréjének leírására az Michaelis-Menten enzimkinetika szolgál. A XX. század elején kidolgozott elmélet tisztázta az enzimek szerepét a folyamatban, geometriai struktúrákkal illusztrálva a molekulák elbontásának mechanizmusát.

6.1‑2. ábra
A lebontás illusztrálása
Egy adott enzim csak egy adott szubsztrát molekula lebontására képes. Ezt jelzik a 6.1-2. ábrán a „zárba illő kulcsot” szimbolizáló geometriai alakzatok. Megfogalmazhatjuk a következő axiómát:
4. axioma
Ahhoz, hogy a lebontás nagy valószínűséggel végbe mehessen a reaktortérben, mintázatában a szubsztráthoz „illeszkedő” enzimnek jelen kell lennie.
A szubsztrát-komplex-termék fázisok reverzibilis és irreverzibilis képződési szakaszai egyenletek, differenciálegyenletek segítségével is leírhatók.
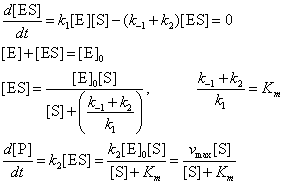

6.1‑3. ábrán
Az enzimkinetika blokkvázlata és egyenletei
A 6.1-3. ábrán vázolt algebrai és differenciál egyenletrendszernek van megoldása. Eredményként a reakciósebességet, a termék képződésének sebességét kapjuk, amely a szubsztrát-tartalom függvénye lesz (lásd 6.1-4. ábra).

6.1‑4. ábra
A reakció sebesség, a megoldás függvény
A levezetett modell egyszerű, a jelenségről jó fenomenológiai leírást ad. A paraméterek vmax és Km jól mérhető mennyiségek. A jelenség telítődéses jellegét a vmax határsebesség, a reakció sebesség növekedésének gyorsaságát pedig az ún. féltelítődési állandó, Km jellemzi.
Biológiai tanulmányainkból azt is tudhatjuk, hogy a lebontás nem egy lépésben történik. Ilyen többlépéses folyamat a nitrifikáció-denitrifikáció egymást követő fázisok sorozata is. Az első reakcióban keletkező termék a következő lépésben szubsztrát lesz. A szakaszos lebontás azzal a veszéllyel jár(hat), hogy a folyamat valahol elakad, nem fejeződik be, hátrahagyva a vízben nem kívánatos, esetleg toxikus anyagokat. Talán emiatt nevezik a biológiai víztisztítást nehezen kézben tarthatónak.
Szokás a lebontási folyamatot sztöchometrikus egyenletek útján is leírni. A végtermék oxikus körülmények között javarészt víz és szén-dioxid lesz. A hidrogén és szén oxidációja „égésként” is felfogható. A reakció során felszabaduló energia azonban jellemzően nem hőenergia - ahogy az a lánggal történő égéseknél tipikus -, hanem kémiai energia, amelyből a sejt a működéséhez, életének fenntartásához szükséges energiát nyeri.
A fentiek alapján következtetés is levonására is vállalkozhatunk:
A mechanikai szűrők visszatartják a szennyezést, a biológiai szűrők ezzel szemben helyben „elégetik” azt. A mechanikai szűrőket – beleértve a membránokat is – rendszeresen tisztítani kell, a biológiai szűrők ezzel szemben nagyrészt öntisztulók. Ez a tény indokolja a biológiai szűrés alkalmazásának előtérbe helyezését minden más eljárással szemben.
6.2 A mikrobák szaporodása
A baktériumok egysejtű élőlények. Testfelépítésük fehérjéből, nukleinsavból, lipidből és vízből áll. A fehérjetartalom jelentős hányada enzimfehérje, amely a tápanyag-lebontás folyamatában – amint azt az előző fejezetben láttuk - katalizátorként működik, szerepe az aktiválási energia lecsökkentésében jelölhető meg.
A baktériumoknak is – mint minden élőlénynek - van egy lényeges tulajdonsága, nevezetesen, hogy szaporodni képesek. A leggyakoribb szaporodási forma az osztódással történő szaporodás. A mikrobaszaporodás kinetikáját a Michaelis-Menten enzimkinetika analógiájára, Monod egy fél évszázaddal később, 1949-ben alkotta meg.
A binárisan osztódással történő szaporodás exponenciális függvény segítségével írható le.

6.2‑1. ábra
Mikrobaszaporodás
bináris osztódással
Az n-k generáció után
ahol x0 a kezdeti x az n.-k generációban a mikrobaszám
mikrobaszámot kapunk. Átrendezve és kifejtve az n generációk számértékére kapunk összefüggést:
A generációk száma kifejezhető az eltelt idő és a generációs idő hányadosaként is:

A generációs idő hosszúsága a szaporodás gyorsaságát jellemzi. Minél rövidebb időről van szó, annál gyorsabban történik a lebontás.
Ez a tárgyalásmód meglehetősen szemléletes ugyan, de az egyes generációs lépések közötti leszámlálások végrehajtása nehézségekbe ütközik, ezért inkább a differenciálegyenlet segítségével történő leírás a szokásos, ahogy azt Monod javasolta.

A konstans relatív növekedésű szaporodást az µM Monod együttható jellemzi, amely az egymást követő generációk sokszorosodásának mértékét mutatja. A (6.2-4) differenciálegyenlet megoldása exponenciális függvényt ad eredményül. A függvény grafikonja az idő növekedésével a végtelenbe tart, ezért a gyakorlatban csak a függvény kezdeti és exponenciális szakaszának elejét használjuk a növekedés leírására.

6.2‑2. ábra
A konstans relatív növekedésű folyamat
A µM kitevő nagysága méréssel határozható meg. Értéke a szubsztrát-tartalom függvényében telítődéses jelleget mutat.

6.2‑3. ábra
A Monod-tényező leírása a féltelítődési állandó segítségével
A formai hasonlóság a Michaelis-Menten kinetika reakciósebességének és a Monod kinetika exponensének szubsztrát függőségének alakulásában fedezhető fel. A görbék növekedési meredeksége a féltelítődési állandók ( ott Km, itt Ks ) megadásával jellemezhető (vesd össze a 6.1-4. és 6.2-3. ábrák lefutási jellegét).
A mikrobák növekedési üteme órás, esetenként napos nagyságrendű. A vizes környezet oldott oxigéntartalmának növekedésével a telítődési érték, µM,max ugyan nagyobbá válik, de a szubsztráttartalomtól függő növekedési ütem – a telítődési görbe meredeksége - érdemben nem változik, ahogy azt a 6.2-4. ábra is mutatja.

6.2‑4. ábra
A Monod-tényező telítődési értékének függése az oldott oxigéntől
A telítődési görbe meredekségét a szubsztrát típusa, az ahhoz mintázatában illő enzim, illetve végsősoron a szaporodó baktériumok fajtája határozza meg.
A generációs idő
a megoldásfüggvények egyezősége alapján könnyen meghatározható, azaz a Monod-tényező és a generációs idő között egyértelmű függvénykapcsolat áll fenn:

A Zárt rendszerek esetében a növekedés azonban korlátozott. E ponton túllépünk a Monod-kinetika állandó növekményre alapozott felfogásán. A (6.2-4) egyenlet korrigált – növekedésében négyzetesen „befékezett” - módosításával a

alakú összefüggést kapjuk. A (6.2-7) differenciálegyenletnek szintén van analitikus megoldása, amelyet a matematikai szaknyelv logisztikai függvényként ismer.

A (6.2-8) függvény grafikonját a 6.2-5 ábra mutatja, amely nem tart a végtelenbe és van exponenciális növekedésű szakasza is. Fontos az a tulajdonsága is, hogy értéke az origóban kicsi, de nem nulla.

6.2‑5. ábra
A logisztikai függvény, a korlátozott növekedési folyamat megoldása
A szilárd felületen megtapadni képes biofilmnek időben több fázisa van (lásd 6.2-6. ábrát). Használva az ábra számozását a megtapadás (1,2), a növekedés (3,4) és a szétszóródás (5) egymást követő periódusai a lét dinamikus jellegéről árulkodnak. A szaporodás és elhalás szakaszai tulajdonképpen fedésbe hozhatók a mikroszkópon látható képekkel (lásd 6.2-6. ábra alsó képkockáit.

6.2‑6. ábra
A biofilm életciklusa a szaporodás és elhalás váltakozásaként
A szaporodás és elhalás egyes fázisait szokás megkülönböztetni is. A gyorsuló, majd lassuló, végül az állandó növekedést pusztulási szakasz követ, ahogy azt a 6.2-7. ábra szemlélteti. A pusztulás a szétszóródással azonos.

6.2‑7. ábra
Szaporodás és elhalás szakaszai
A szaporodás növekedési és állandósuló szakaszai a logisztikai függvény segítségével matematikai formába is önthető. Ehhez csak az (6.2-8) egyenlet x0, K és μM paraméterek helyes megválasztása és kimérése szükséges. A pusztulási fázist a logisztikai függvény nem képes leírni (vesd össze a 6.2-5. és 6.2-7. ábrákat), ugyanúgy, ahogy a Monod kinetika végtelenbe tartó szakasza sem használható a szaporodás véges térben történő jellemzésére.
A Monod-kinetika kapcsán érdemes azt is észrevenni, hogy nulla szubsztrát esetén nincs szaporodás. Ez azt jelenti, hogy a tápanyag szegény víz mikrobiológiai értelemben stabil. Azt a folyamatot, amely a tápanyaghiányt a vízben előidézi fertőtlenítésnek kell tekinteni. Bővebben lásd Függelék 3-ban.
Következmény
A partiszűrés tehát nem csak tisztítja a vizet, hanem egyben fertőtleníti is. Ez akkor is így van, ha a tápanyagelvonást általában nem tekintik fertőtlenítésnek.

