3. A TÁPANYAG-LEBONTÁSI FORMULA
3.1 A dimenzióanalízis lépései
Sok változótól függő, összetett jelenségek – ilyen a partiszűréses víznyerés is – modellezése a dimenzióanalízis segítségével történhet. Szűcs Ervin megfogalmazása szerint:
A dimenzióanalízist akkor és csak akkor érdemes használni, ha
-
nem ismert a rendszer matematikai modellje,
-
de ismertek a rendszerben végbemenő folyamatok változói.
A probléma felvetése és a működésmód előzetes feltérképezése után megkísérelhetjük a tápanyag-lebontási összefüggés levezetését. A következőkben az Függelék 1-ben bemutatott hasonló feladat példáján haladva, a dimenzióanalízis eszközeivel próbálunk célt érni. Ehhez Szirtes Tamás módszerét használjuk.
A lebontási folyamat összefüggésének megfogalmazásához először számba kell vegyük a folyamatot leíró változókat. A változók legyenek rendre:

Az egyetlen függő változót – esetünkben a ΔS tápanyag-lebontási mértéket – a dimenzióanalízis módszertanának megfelelően a felsorolás elején kell szerepeltetni.
Második lépésként az ún. dimenziómátrix felvázolása a feladat. A dimenziómátrix oszlopait a jelenséget leíró változók, sorait azok mértékegysége adja.
A 3.1‑1. ábra vastag vonal feletti része a dimenziómátrix, amelyből jobbról kihasítunk egy négyzetes részt (A). A fennmaradó hányad (B).

3.1‑1. ábra
A tápanyag-lebontás folyamatának dimenzió- és eredménymátrixa

A következő lépés a dimenziómentes számok kiolvasása az eredménymátrixból, amelyek rendre

A dimenzióanalízis eddigi lépései a változószám csökkentését eredményezték. Kezdetben 10 változónk volt, amely mostanra 4-re redukálódott. Tulajdonképpen az eredeti még dimenzióval bíró változók dimenziótlan számokba sűrűsödtek.
Az eljárás további részében a már számukban lecsökkent dimenziómentes változók közötti összefüggést keressük, amely. általános alakban a következő formát ölti:
ahol ψ a keresett, ismeretlen függvény.
A keresett függvénykapcsolat: monom (egytagú) vagy polinom (többtagú) alakú lehet. Az általánosság különösebb megszorítása nélkül a természettörvények azonban nagyon gyakran tényezők szorzataként előálló egytagú kifejezések. Tételezzük hát fel – tovább szűkítve a lehetőségeket -, hogy a keresett függvénykapcsolat, a tápanyag-lebontásának törvényszerűsége monom alakú, azaz a következő általános képletnek megfelelő:
Belyettesítve a kapott dimenziómentes változókat, majd ΔS-re rendezve a következő kifejezéshez jutunk:

A feladat ezek után a dimenziótlan µ együttható és az ε2, ε3, ε4 kitevők értékének kimérésére vagy becslés útján történő meghatározására egyszerűsödik. A továbbiakban heurisztikus megállapítások segítségével az említett négy paraméter (az együttható és a három kitevő) értékének meghatározásakor az ilyenkor szokásos heurisztikus módszert alkalmazzuk. Rávezető megfontolások alapján megpróbáljuk kitalálni a még ismeretlen paramétek értékét.
3.1.1 ε2 megválasztása
A partiszűrés változó sebességű szűrés. A w szűrési sebesség a szűrési útvonal elején, a mederkapcsolatnál – a legkisebb. A megfigyelések szerint éppen itt figyelhető meg biológiai aktivitás, itt alakul ki a biofilm. A kút közvetlen közelében a vízadó rétegben érzékelhető vízsebesség már relatíve nagy. Ehelyütt nem figyelhető meg biológiai tápanyag-lebontás. Joggal tételezhetjük fel, hogy a biológiai tápanyag-lebontás mértéke a szűrési sebességgel fordított arányosságban áll, azaz ε2 = -1 választás a kívánatos. De vajon helyes-e ez a választás a többi tényező tekintetében is?
Kisebb szemcsék között a diffúziós úthossz is rövidebb, ahogy a 2.2-2. ábrán szemléletes módon megfigyelhetjük. A rövidebb diffúziós úthossz a tápanyag gyorsabb bejutását teszi lehetővé és így a lebontás ütemét érdemben befolyásolja. A szemcseátmérővel való fordított arányosságot ugyancsak az ε2 = -1 választással fejezhetjük ki.
A biofilm tulajdonságainak leírásánál láttuk, hogy a tápanyagnak be kell jutnia a biológiai hártyába. Ez annál könnyebben valósulhat meg minél nagyobb a diffundáló tápanyag diffúziós tényezője.
A különböző anyagok diffúziós tényezője (1 ... 20) *E-10 m2/s tartományban változik. A diffúziós tényező számértékét 25 °C hőmérsékleten adják meg. A diffúziós tényező értéke a hőmérséklet növekedésével nő. A szorzótényező minden anyag esetén azonos.

3.1-2. ábra
A diffúziós tényező hőmérséklet függése 0 -30 °C tartományban
A szerves anyag koncentrációjának csökkenése (ΔS), avagy a tápanyag-lebontás mértéke tehát arányos kell legyen a diffúziós tényezővel. Ennek megfelelni ugyancsak választással tudunk ε2 = -1 választással tudunk. .
Úgy tűnik tehát, hogy a Pe dimenziótlan szám mindhárom tényezője – dm, w és Ds - esetében az ε2 = -1 hatványkitevő minden szempontnak megfelelő helyes választás.
A (3.1-3) kiindulási képlet az alábbiak szerint pontosodik:

3.1.2 ε3 lehetséges értéke
A dm mértékadó szemcseátmérőre tettünk már kijelentést, miszerint a diffúziós úthossz kisebb szemcseméret esetén kisebb. Egy másik megfontolás szerint adott partszakaszon a felület akkor nagyobb, ha minél kisebb a biofilmet hordozó szemcsék átmérője. Ugyanakkora térfogatban a kisebb homokszemcsék nagyobb felülettel rendelkeznek, mint az átmérőjükben nagyobb kavicsok. A baktériumok a gömbnek tekintett szűrőréteg szemcséin telepedhetnek meg. Minél nagyobb ez a felület, annál több baktériumnak van helye. A felület nagysága a szemcseátmérő négyzetével fordítottan arányos. Ezt matematikailag az ε2- ε3 = -2 egyenlettel fejezhetjük ki.
Miután ε2 = -1 -t már más megfontolások alapján rögzítettük, így a kitevőkre vonatkozó képlet alapján ε1 =1 adódik.
Ez a választás egyben azt is jelenti, hogy a tápanyag lebontás mértéke az aktív réteg vastagságtól La egyenes arányban függ. Vastagabb rétegben több baktérium telepedhet le. Ez a következmény nem áll szemben a megfigyelésekkel.
A kialakuló aktív réteg azonban nem nő a végtelenségig. Ezt a 2005-ben lefolytatott Jekel-kísérletek mérésekkel igazolták:

3.1‑3. ábra
A Jekel kísérlet eredménye
A 3.1-3. ábrán az oldott szerves szén, DOC (Dissolved Organic Carbon) a szűrési útvonal mentén mind oxikus, mind anoxikus viszonyok közepette előbb csökken, majd állandósul. Az útszakasz elején a csökkenés mértéke erőteljes, az első 5 -10 méter után a biológiai tápanyag-lebontás állandósul. A biológiailag aktív réteg La vastagsága tehát korlátos.
A 3.1-3. ábra viszonyait némileg idealizáltan át is rajzolhatjuk. A szokásos paraméterek megadásával a mért görbement idealizáltan is megrajzolható (lásd 3.1-4. ábra). A DOC fogyást most általában S szubsztrát fogyásnak feltüntetve.

3.1‑4. ábra
Lebontás a szűrési útvonal mentén idealizáltan
La,∞ után a szubsztrát tovább már nem fogy, a szűrési útvonal további szakasza már nem vesz részt a víztisztulási folyamatban.
Tápanyag-lebontási képletünk így tovább konkretizálódik:

3.1.3 ε4 valószínű számértéke
Az Ne* = (Eh F) / (R T) -tényezőben F és R fizikai állandók. A T abszolút hőmérséklet számértéke csak pozitív lehet. A biológiai szűrés jellemző hőmérsékleti tartományát a T = 273…303 K intervallumra vetíti. T változása az abszolút hőmérsékleti skálán relatív tekintetben tehát nem nagy.
A redoxpotenciál Eh értéke ezzel szemben pozitív és negatív is lehet. valószínű számértékének becslésekor pusztán matematikai megfontolásokból is kiindulhatunk. A hatvány függvények grafikonja alapján számos hatványkitevő érték kizárható (részletesebben lásd Szemengyajev-Bronstein : Matematikai zsebkönyv / Függvénygrafikonok / Elemi függvények fejezetben) Miután a hőmérséklet Ne*-tényező képletében a nevezőben szerepel, az ε4 < 0 választás visszatükrözné a magasabb hőmérséklet – magasabb biológiai aktivitás érzetet. Ez esetben azonban a számlálóban szereplő Eh-tól való függés hiperbolikus jelleget mutatna, azaz Eh = 0 környezetében a függvény értéke végtelenbe szaladna. Ennek nem volna sem fizikai, sem biológiai magyarázata, ezért csak pozitív ε4 értékek jöhetnek szóba. Kizárhatók továbbá az 1-nél nagyobb értékek is.
A redoxpotenciál előjelváltásából, valamint abból az igényből, hogy a keresett tápanyag-lebontási összefüggés tükrözze vissza az oxikus / anoxikus jelleget, úgy hatvány függvényünk kitevője csak páratlan lehet, azaz ε4 = 1/3, 1/5, 1/7, … közül válaszhatunk. A valószínű érték azonban az
ε4 = 1/3 lesz. A választás megalapozásához további megfontolásokat kell tenni. (Lásd később 5. Biológiai szűrés környezeti viszonyai fejezetben) ε4 megválasztásával így a (3.1-6) formula már csak egyetlen ismeretlent tartalmaz:

Visszahelyettesítve a dimenziótlan számokat

már majdnem a végleges összefüggést kapjuk.
3.1.4 A µ együttható definiálása
A µ együttható interpretálásához a (3.1-7) függvény grafikonjából indulunk ki. A formula alapvetően két – a Pe-számtól függő és a Pe-számtól nem függő – részre osztható:
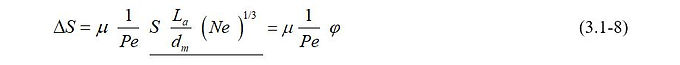
A Pe számtól függő rész a fizikai transzport folyamatot, azaz a logisztikai előfeltételt írja le, míg a többi tényező - φ-ben összevontan - a tápanyag-lebontás biokémiai viszonyaira utal, vagy másképpen a jelenség környezeti („klimatikus”) vonatkozásairól szól. A tápanyag-lebontásához a biofilmen kívüli logisztikai előfeltételnek ugyanúgy teljesülnie kell, mint a biofilmen belüli körülményeknek. A (3.1-8) képletben a két tényező szorzata éppen ezt fejezi ki.
Ábrázolva a (3.1-8) függvénykapcsolatot hiperbolasereget kapunk. Az egyes hiperbolákat több tényezőt magába foglaló φ paraméter különíti el.

3.1‑5. ábra
A tápanyag-lebontási görbe jellege
Kis Pe-számnál a hiperbolák függvényértéke a végtelenbe tart. Határtalanul nagy tápanyag-lebontás azonban kis Pe-számok tartományában nem képzelhető el. A függvény értékét az origóban alacsonyra várjuk, ahogy ezt a kívánalmat a 3.1-5. ábrán a piros görbe jelzi. Az alapvetően hiperbolikus görbemenet „eltérítéséhez” a µ = µ(Pe) függvénykapcsolatnak kell fennállnia. A µ szűrési tényező Pe-szám függésének megadásához további megfontolások szükségesek (lásd később 6. A biofilmen belüli biokémiai folyamatok fejezetben). A µ együttható megadásával a tápanyag lebontási formula teljessé válik majd.

